| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 삼성SW역량테스트
- html태그정리
- html input
- html환경구축
- RAID구축
- RAID개념설명
- Linux
- 멀티캐스트
- jupyter
- TensorflowServer
- 개념설명
- HTML예제
- raspberrypi
- C언어
- Ubunrtu
- html input tag
- 다항회귀예제
- 코딩테스트후기
- 다항회귀
- 삼성sw역량테스트b형
- RIAD0
- HTML
- Raid
- docker
- 라즈베리파이
- ubuntu18.04
- CSS
- multicast
- tensorflow
- 웹페이지 기본
- Today
- Total
Easy ways
[python]다항회귀(Polynomial Regression)란? [예제 포함] 본문
안녕하세요
오늘은 요즘 AI 쪽에서도 많이 사용되는 다항 회귀를 공부해 볼까합니다.
살다보면 많은 데이터를 마주하게 되는데요
데이터를 분석하다보면 선형적인 그래프로 데이터를 표현하기 어려운 경우가 생깁니다.
이를 비선형 데이터라고 부릅니다.
사실 세상 대부분의 데이터들은 비선형 데이터죠
이러한 비선형 데이터를 학습하기 위해 다차원 식을 만드는 기법을 다항회귀라고 합니다.

쉽게 말해서 이 데이터가 어떠한 추이를 보이고 있는데
이게 선형 즉 직선으로 표현할 수 없을 때, 다항회귀를 사용하게 됩니다.
오늘은 이러한 다항회귀에 대해 함께 공부해보겠습니다.
다항 회귀(Polynomial Regression)란?
다항 방정식은 다음과 같은 공식으로 표현할 수 있습니다.

직선으로 어떤 데이터를 충분히 표현하지 못하는 데이터는
데이터의 편향(bias)이 크다고 표현합니다.
반대로 다항 회귀에서는 차수가 너무 큰 경우에는 변동성이 커지고, 이를 고분산성을 가진다고 합니다.
차수가 높아질 수록 복잡성 또한 높아지겠죠,
편향 (bias) 과 분산(Variance)은 한쪽 성능을 좋게 하면, 나머지 하나의 성능이 떨어지는 관계에 있습니다.
이 둘의 성능을 적절하게 맞춰 전체 오류가 낮아지는 지점을 골디락스 지점이라고 합니다.
python sklearn 을 사용한 다항 회귀 예제
이제 실제로 다항회귀가 어떻게 동작하는지에 대해 알아보기 위해 예제를 한번 풀어보겠습니다.
예제를 위하여,
대중적으로 사용하는 python sklean 을 사용하겠습니다.
Sklearn 의 Polynomial Regression 모델은
비선형 데이터를 학습하기 위해, 선형 회귀 모델을 사용하는 기법입니다.
어떤 식으로 동작하는지는 아래 예제를 통해 자세히 알아보도록 하겠습니다.
데이터 수집 및 확인
다항회귀 예제에 적합한,
추이가 보이면서 비선형적인 데이터는 뭐가 있을까요?
저는 키와 몸무게가 적합하다고 생각하여
공공데이터 포털에서 제공하는 학생들 키와 몸무게 파일을 통해서 한번 진행해보겠습니다.
아래 링크에서 다운로드 받으시면 됩니다.
https://www.data.go.kr/data/15051017/fileData.do

csv 파일을 다운받아 풀어보면 위와같이 학생의 키와 몸무게 뿐만아니라 다양한 데이터가 표기되어있습니다.
우선 키와 몸무게의 상관관계부터 확인을 해보겠습니다.
import pandas as pd
import matplotlib.pyplot as plt
filename = '교육부_학생건강검사 결과_20151201.csv'
df = pd.read_csv(filename, encoding='cp949')
df = df.reset_index()
# 불필요한 칼럼 제거
df = df[['몸무게','키']]
# Nan 데이터 제거(공백 데이터)
df = df.dropna()
weight = []
height = []
# 키와 몸무게 칼럼 추출
weight.extend(df['몸무게'])
height.extend(df['키'])
plt.figure()
plt.scatter(weight,height, alpha=0.3,color = 'orange')
plt.title('Realation of weight and height')
plt.xlabel('weight')
plt.ylabel('height')
plt.show()

자, 상관관계가 확실한 데이터를 얻었습니다.
직선으로 표현하기에는 어려워 보입니다.
다항회귀 사용에 적합해보이네요
이제 이 데이터를 통해 다항회귀를 진행해 보도록 하겠습니다.
sklearn을 사용한 다항회귀(Polynomial Regression)
우선 기본 전체 코드는 아래와 같습니다.
# -----------------------------------------------------------
# Purpose : Study For Polynomial Regression
# Date : 2022/07/22
# PROGRAMMER : softColor
# -----------------------------------------------------------
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np
filename = '교육부_학생건강검사 결과_20151201.csv'
df = pd.read_csv(filename, encoding='cp949')
df = df.reset_index()
# 불필요한 칼럼 제거
df = df[['몸무게','키']]
df = df.dropna()
weight = []
height = []
# 키와 몸무게 칼럼 추출
weight.extend(df['몸무게'])
height.extend(df['키'])
# PolynomialFeatures 에 맞게 데이터를 변형 시켜줍니다.
weight_real =np.reshape(weight,(-1, 1))
# 몇 차 다항식을 할 것인지 선택합니다.
user_degree = 3
print('degree: ', user_degree)
# x 에 대한 제곱근 (다항식 형태로 변환)
poly_features = PolynomialFeatures(degree=user_degree, include_bias=False)
X_train_poly = poly_features.fit_transform(weight_real)
print('real weight : ',weight_real[0])
print('poly : ',X_train_poly[0])
#다항 회귀 예측
lin_reg = LinearRegression()
lin_reg.fit(X_train_poly, height)
print('intercept : ',lin_reg.intercept_,', coef:' , lin_reg.coef_)
X_new=np.linspace(15, 130, 100).reshape(-1, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
print('===============================================')
plt.figure()
plt.scatter(weight, height, alpha=0.3, color ="orange")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
plt.title('Polynomial Regression by weight and height(degree = %d) '%user_degree)
plt.xlabel("weight")
plt.ylabel("height")
plt.legend(loc="upper left")
plt.show()
위 코드를 돌리면 다음과 같은 그래프가 출력됩니다.

좀 그럴듯 해보이나요?
제 눈에는 데이터를 충분히 잘 표현하고 있다고 생각됩니다.
이제, 코드를 하나씩 뜯어보겠습니다.
핵심부분은 다음과 같습니다.
poly_features = PolynomialFeatures(degree=user_degree, include_bias=False)
X_train_poly = poly_features.fit_transform(weight_real)PolynomialFeatures 옵션
- degree : 차수 조절
- include_bias : True로 할 경우 0차항(1)을 만듬
저의 경우는 차수는 3차항으로, 그리고 0차항은 제외하고 만들었습니다.
이렇게 만들어진 다항식 모델에 x를 fit transform하여 새로운 데이터를 생성합니다.
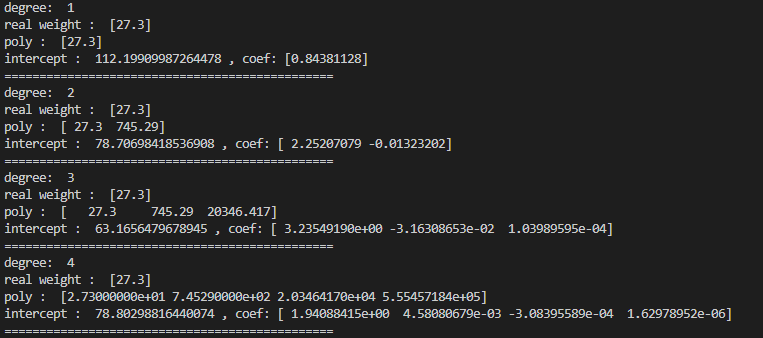
데이터를 확인해보면 조금 더 이해가 쉽습니다.

그럼 입력한 데이터와 차수값이 표출됩니다.
저의 경우 3차항 까지의 값, 즉 x의 세제곱 값까지 나타난 것을 볼 수 있습니다.
입력데이터 x
x가 27.3이고
x^2 인 745.29
x^3 인 20346.417
이러한 배열이 X_train_poly에 들어가게 됩니다.
lin_reg = LinearRegression()
lin_reg.fit(X_train_poly, height)
print('intercept : ',lin_reg.intercept_,', coef:' , lin_reg.coef_)다음으로 y값 입력을 통해 Linear regression, 선형 회귀를 합니다.
선형 회귀를 하게되면 입력한 데이터들에 대한 공식을 표출 할 수 있게됩니다.
- line_fitter.coef_: 기울기, 다항회귀 공식의 a_1, a_2,..,a_s
- line_fitter.intercept_ : 절편, 다항회귀 공식의 a_0


저의 경우는,
절편은 63.xxxx, 기울기는 3.23xxx, -3.16xxx, 1.03xxx 이렇게 출력되었네요.
키 몸무게 입력을 통해 만들어낸
Linear regression 결과값을 수식으로 표현하면 다음과 같습니다.

이 수식이 맞는지 확인을 위하여 수식을 코드로 작성하여 다시 실행해봤습니다.
x_new=np.linspace(15, 130, 100).reshape(-1, 1)
y_new = 63.1656479678945+(x_new*3.23549190e+00)+(-3.16308653e-02*x_new**2)+(1.03989595e-04*x_new**3)
plt.plot(X_new, y_new, "b--", linewidth=2, label="Predictions")
plt.show()
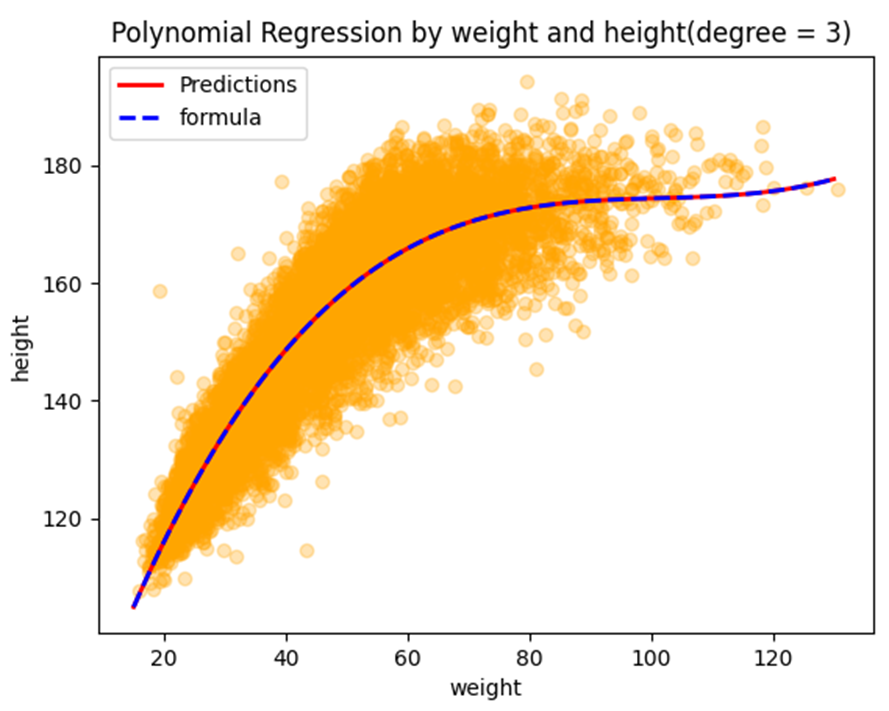
정확하게 일치하는 모습을 볼 수 있습니다.
이외에도 다양한 시도를 해봤습니다.

4차 다항식 부터 그래프가 조금 벗어나기 시작합니다.
아싸리 아예 높여볼까요.

정확도는 높아졌지만 복잡성이 높아진 모습을 볼 수 있습니다.
이러한 식으로 적절한 차수와 항을 찾아가 자기만의 적정 모델을 만들어보시죠!
참조
https://inuplace.tistory.com/515
https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PolynomialFeatures.html
'개념정리' 카테고리의 다른 글
| [개념정리] 빅엔디안(Big Endian)과 리틀엔디안(Little Endian) (0) | 2021.03.24 |
|---|---|
| 멀티캐스트(multicast)란? [feat. 브로드캐스트(broadcast)] (1) | 2021.02.05 |
| RAID 란?? (0) | 2020.11.10 |



